Question

7. A right triangle has a hypotenuse of 13 and a leg of 8. What is the other leg? Show your work.

Answer 1

Answer:

the other leg is √105

Step-by-step explanation:

Given:

Hypotenuse = 13

one of the legs of the triangle = 8

To find:

the other leg of the triangle

The triangle is right-angled. So, to get the third side, we will apply Pythagoras theorem:

Hypotenuse² = opposite² + adjacent²

let opposite = leg 1 = 8

adjacent = leg 2

Hypotenuse² = = leg1² + leg2²

`\begin{gathered} 13^2=\text{ 8}^2\text{ + leg}_2^2 \\ \\ 169\text{ = 64 + leg}_2^2 \\ \\ 169\text{ - 64 = leg}_2^2 \\ \\ 105\text{ = leg}_2^2 \end{gathered}`
`\begin{gathered} square\text{ root both sides:} \\ √(105)\text{ = leg}_2 \\ Can^(\prime)t\text{ be reduced an further inradical form} \\ \\ leg_2\text{ = }√(105)\text{ } \end{gathered}`

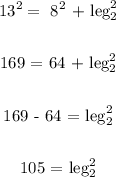
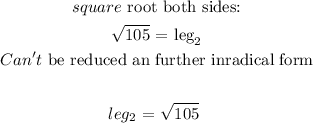
Hence, the other leg is √105