In a unit circle every angle is measured from the positive x-axis to its terminal line traveling counterclockwise; the reference angle is the smallest possible angle formed by the x-axis and the terminal line going either clockwise or counterclockwise.
Now, to find the reference angle we first need to determine in which quadrant the original angle is; then, depending on where the angle is, we calculate the reference angle by remembering the following rules:
• If the original angle is in the first quadrant then the reference angle is the same.
,
• If the original angle is in the second quadrant then the refrence angle is found by the formula:
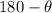
• If the original angle is in the third quadrant the reference angle is given by:
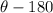
• If the original angle is in the fourth quadrant the reference angle is given by:
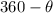
Now that we know this let's find the reference angle for 245°. This angle is in the third quadrant, and hence its reference angle is:
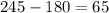
Therefore, the reference angle is 65°