Question

For the three-part question that follows, provide your answer to each question in the given workspace. Identify each part with a coordinating response. Be sure to clearly label each part of your response as Part A, Part B, and Part C.Part A: Write a function in for the geometric sequence where the first term is 11 and the common ratio is 4 .Part B: Find the first five terms in the geometric function.Part C: In one paragraph, using your own words, explain your work for Step A and Step B.

Answer 1

Remember that the formula for a geometric sequence is:

`a_n=a_1\cdot r^(n-1)`

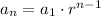
PART A:

With the data given, the formula for the sequence is:

`a_n=11_{}\cdot4^(n-1)`

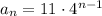
PART B:

`\begin{gathered} a_1=11\cdot4^(1-1)\rightarrow a_1=11 \\ a_2=11\cdot4^(2-1)\rightarrow a_2=44 \\ a_3=11\cdot4^(3-1)\rightarrow a_3=176 \\ a_4=11\cdot4^(4-1)\rightarrow a_4=704 \\ a_5=11\cdot4^(5-1)\rightarrow a_5=2816 \end{gathered}`

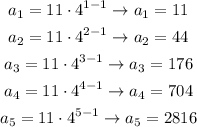
PART C:

For part A, we took the general formula for the geometric sequence and plugged in the first term and the common ratio provided.

For part B, we replaced n for all the numbers from 1 through 5 to get the first 5 terms of the sequence.