Step-by-step explanation:
Given;
We are given a triangular pyramid with the following dimensions;
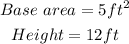
Required;
We are required to calculate the volume of this pyramid from the dimensions given.
Step-by-step solution;
The volume of a triangular pyramid is given by the formula;
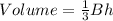
Where the variables are;
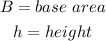
The volume now will be calculated as follows;
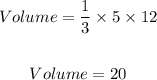
Therefore,
ANSWER:
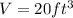
Volume = 20 cubic feet