ANSWER
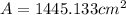
Step-by-step explanation
We have to find the surface area of the composite figure made of a hemisphere and a cone.
To do that, we have to find the curved surface area of the hemisphere and the curved surface of the cone and add them together.
We are using curved surface area since the area of the flat surfaces of the cone and hemisphere are not relevant since they are covered.
The curved surface area of a hemisphere is given as:
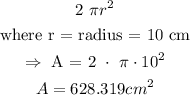
The curved surface area of a cone is given as:
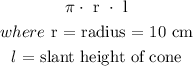
We can get the slant height of the cone by using Pythagoras rule:
So, we have:
![\begin{gathered} l^2=10^2+24^2\text{ = 100 + 576} \\ l^2\text{ = 676} \\ l\text{ = }\sqrt[]{676} \\ l\text{ = 26 cm} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gngrpalzjrumg84tb3j5ph3r6g4gdah5pr.png)
So, the curved surface area of the cone is:
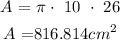
Now, adding them together, the surface area of the composite figure is:
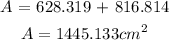
That is the answer.