The absolute value function :
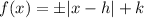
has a vertex at (h, k) and it opens upward if the sign before the absolute value sign is positive. It open downward if the sign is negative.
From the problem, we have :
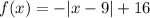
The vertex will be (9, 16)
x intercept is the value of x when f(x) = 0.
Set f(x) = 0 and solve the value of x.
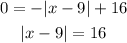
In solving absolute values, you will get two values, one for the positive and one for the negative.
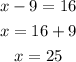
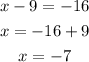
The x-intercepts are (-7, 0) and (25, 0)
y-intercept is the value of f(x) when x = 0.
Set x = 0, and evaluate f(x)
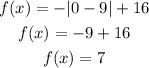
The y-intercept is (0, 7)
The sign before the absolute value sign is negative, so it opens downward