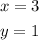Question

Just need help understanding how to do these step by step explanation please

Answer 1

Given the simultaneous equations:

`\begin{gathered} 4x+3y=15\text{ --- equation 1} \\ 5x-2y=13\text{ ---- equation 2} \end{gathered}`

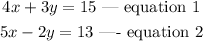
To solve for x and y, using the elimination method, we have

`\begin{gathered} 2*(4x+3y=15)\Rightarrow8x+6y=30\text{ --- equation 3} \\ 3*(5x-2y=13)\Rightarrow15x-6y=39\text{ --- equation 4} \end{gathered}`

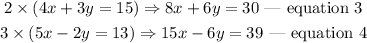
Add up equations 1 and 2.

thus, this gives

`\begin{gathered} 8x+15x+6y-6y=30+39 \\ \Rightarrow23x=69 \\ divide\text{ both sides by the coefficient of x, which is 23} \\ (23x)/(23)=(69)/(23) \\ \Rightarrow x=3 \end{gathered}`

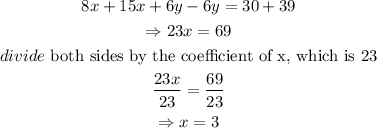
To solve for y, substitute the value of 3 for x into equation 1.

thus, from equation 1

`\begin{gathered} 4x+3y=15 \\ when\text{ x = 3,} \\ 4(3)+3y=15 \\ \Rightarrow12+3y=15 \\ add\text{ -12 to both sides,} \\ -12+12+3y=-12+15 \\ 3y=3 \\ divide\text{ both sides by the coefficient of y, which is 3} \\ (3y)/(3)=(3)/(3) \\ \Rightarrow y=1 \end{gathered}`

Hence, the solution to the equation is

`\begin{gathered} x=3 \\ y=1 \end{gathered}`