Area of a Triangle
Given a triangle of base length B and height length H, the area can be calculated by the formula:
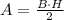
The base and the height must be perpendicular.
The height of the given triangle is H=7 in. We need to calculate the length of the base.
We are providing a new image where a variable x is introduced to help us calculate the base length:
The triangle formed by the sides 9-7-x is right, so we can calculate the value of x by applying the Pythagora's Theorem:
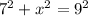
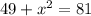
Solving for x:
![\begin{gathered} x^2=81-49=32 \\ x=\sqrt[]{32} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rdreh5nmzxmjqqsfot4jztuk5yazheoqsq.png)
The length of the base is:
![B=9+\sqrt[]{32}](https://img.qammunity.org/2023/formulas/mathematics/college/hwr6aromkv7al48ua5pj0nw9j1ac7f139y.png)
Thus, the area of the triangle is:
![A=\frac{7\cdot(9+\sqrt[]{32})}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/ztxixw357zvq0l7k938u2cf10sncars4np.png)
Calculating:
A = 51.3 square inches