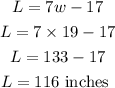SOLUTION
We are told that the length of the rectangle is 17 inches less than 7 times its width.
Now, let the letter L represent the length and the letter w represent the width of the rectangle.
This statement can be represented algebraically as
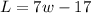
So, Area =
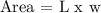
We are also told the Area A of the rectangle = 2204. Now
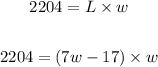
We have to find the width, then we find the length L
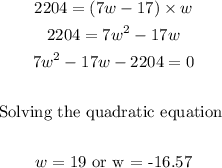
Since the width cannot be negative, w = 19 inches
The length becomes