EXPLANATION
Given the function y=-2x^2 -12x -5
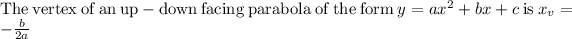
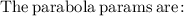
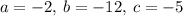
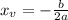
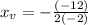
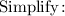
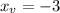
Plug in x_v=-3 to find the y_v value:
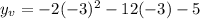
Computing the powers and multiplying terms:
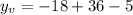
Adding and subtracting numbers:
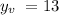
Therefore, the parabola vertex is:
(-3,13)
Now, we need to compute the y-intercept
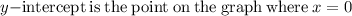
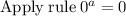
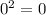
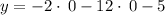
Multiplying numbers:
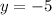
The y-intercept is at (0,-5)
In conclusion, the graph of the function is as follows: