Question

The coordinates of the midpoint of GH are M(-2,5) and the coordinates of one endpoint are H(-3, 7).

The coordinates of the other endpoint are(
).
Echeck
? Help
< PREV - 1 2 3 4 5 6
-
NEXT >
What are the coordinates of the other endpoint

Answer 1

EXPLANATION :

From the problem, we have segment GH and the midpoint is M(-2, 5).

One of the endpoints has coordinates of H(-3, 7)

and we need to find the coordinates of G(x, y)

The midpoint formula is :

`M=((x_1+x_2)/(2),(y_1+y_2)/(2))`

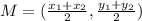
where (x1, y1) are the coordinates of G

(x2, y2) = (-3, 7) are the coordinates of H

and (-2, 5) are the coordinates of the midpoint.

Then :

`(-2,5)=((x+(-3))/(2),(y+7)/(2))`

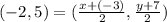
We can equate the x coordinate :

`\begin{gathered} -2=(x+(-3))/(2) \\ \\ \text{ cross multiply :} \\ -2(2)=x-3 \\ -4=x-3 \\ -4+3=x \\ -1=x \\ x=-1 \end{gathered}`

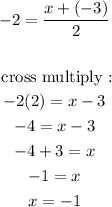
then the y coordinate :

`\begin{gathered} 5=(y+7)/(2) \\ \\ \text{ cross multiply :} \\ 5(2)=y+7 \\ 10=y+7 \\ 10-7=y \\ 3=y \\ y=3 \end{gathered}`

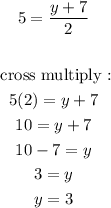
Now we have the point (-1, 3)

ANSWER :

The coordinates of the other endpoint are G(-1, 3)