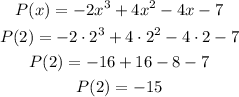Question

Use the factor theorem to determine whether x-2 is a factor

Answer 1

Factor theorem is usually used to factor and find the roots of polynomials. A root or zero is where the polynomial is equal to zero. Therefore, the theorem simply states that when f(k) = 0, then (x – k) is a factor of f(x).

In this case here, let's find out if 2 is a root of the polynomial given.

As we can see in the box below, 2 is not a root of the polynomial, therefore (x-2) isn't a factor.

`\begin{gathered} P(x)=-2x^3+4x^2-4x-7 \\ P(2)=-2\cdot2^3+4\cdot2^2-4\cdot2-7 \\ P(2)=-16+16-8-7 \\ P(2)=-15 \end{gathered}`