Question

A bottle rocket is launched straight up. Its height in feet (y) above theground x seconds after launch is modeled by the quadratic function: y =-16x2 + 132x + 6.How many seconds did it take the rocket to reach its maximum height?

Answer 1

(C)4.125 seconds

Step-by-step explanation:

The quadratic function modeling the rocket's movement is:

`y=-16x^2+132x+6`

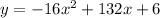
To determine the number of seconds it takes the rocket to reach its maximum height, we are being asked to find the equation of the line of symmetry.

For a quadratic function of the form y=ax²+bx+c, the equation of the line of symmetry is:

`x=-(b)/(2a)`

In the given equation:

a = -16, b = 132

Therefore:

`\begin{gathered} x=-(132)/(-2*16) \\ x=4.125 \end{gathered}`

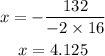
It takes the rocket 4.125 seconds to reach its maximum height.