Answer
LA = 4√10
TA = 4 + 4√10
Explanation
To find the Lateral Area (LA) of the pyramid, first, we need to calculate its slant height (s).
Considering the right triangle formed inside the pyramid, we can apply the Pythagorean theorem to find the length of s, as follows:
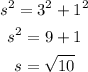
Now, we can calculate the lateral area as follows:
![\begin{gathered} LA=(1)/(2)* P\operatorname{*}s \\ \text{ where P is the perimeter of the base of the pyramid. Substituting }P=4*2\text{ and }s=√(10): \\ LA=(1)/(2)\operatorname{*}4\operatorname{*}2\operatorname{*}√(10) \\ LA=4√(10) \end{gathered}]()
To find the total area (TA) of the pyramid, first, we need to calculate the area of its base (B). In this case, the base is a square, then its area is:

Finally, the total area is calculated as follows:
