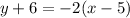Question

Determine the equation of a line in point slope that passes through (5, -6) and (-1, 6)?

Answer 1

First, let's take a look at the point-slope form of a line:

`y-y_0=m(x-x_0)`

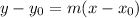
Where:

• m, is the ,slope, of the line

,

• (Xo,Yo) ,is a point that belongs to the line

Now, let's calculate the slope of our line with the poins given:

`\begin{gathered} m=(6-(-6))/(-1-5)\rightarrow m=(6+6)/(-6)\rightarrow m=(12)/(-6) \\ \\ \rightarrow m=-2 \end{gathered}`

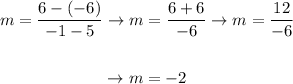
Using this slope and point (5,-6), we'll get the equation of our line in the point-slope form.

`y-y_0=m(x-x_0)\rightarrow y-(-6)=-2(x-5)\rightarrow y+6=-2(x-5)`

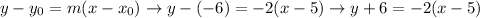
The equation of the line is the following:

`y+6=-2(x-5)`