Answer:
The 99% confidence interval is
7.558 - 9.042
Step-by-step explanation:
The formula for the confidence interval is:
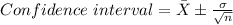
Where:
X is the mean
σ is the standard deviation
z is the z-score for the confidence interval
n is the sample size.
Also, the interval has:
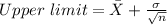
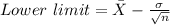
Then, in this case,
The sample size is n = 64
The mean is X = 8.3
The z-score for a 99% confidence interval is z = 2.58
The standard deviation is σ = 2.3
Then:
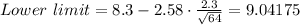
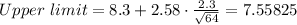
Thus, the confidence interval, rounded to 3 decimals is
7.558 - 9.042