Question

For each of the following letters, find the equation for a polynomial function whose graph resembles the given letter: U, N, M, and W.

Answer 1

We are asked to determine polynomic functions which graph resembles the given letters.

For the letter U we will use a second-degree polynomial, which means a polynomial of the form:

`y=ax^2+b`

Is we take the values of "a" and "b" to be:

`\begin{gathered} a=1 \\ b=0 \end{gathered}`

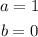
We get the function:

`y=x{}^2`

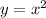
The graph is the following:

Now, to determine a function that resembles the letter N we will use a polynomic function of third-degree, this means a function of the form:

`y=ax^3+bx^2+cx+d`

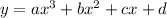
We will use the following values for the constants:

`\begin{gathered} a=(1)/(4) \\ \\ b=1 \\ c=0 \\ d=0 \end{gathered}`

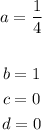
Substituting we get:

`y=(1)/(4)x{}^3+x^2`

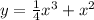
The graph of the function is:

To determine a polynomial that resembles the letter "m" we will use a polynomial that has 3 x-intercepts and the end-points are pointing down. This means that the function is of the form:

`y=-(x-a)(x-b)^2(x-c)`

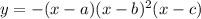
The middle term has a square because we want the middle intercept to be tangent to the x-axis. Giving values to the constant we get:

`y=-(x+1)(x-1)^2(x-3)`

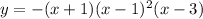
The graph of the function is:

Now, we determine a function that resembles the letter "W". We will use a polynomial with two intercepts that are tangent to the x-axis and the end behavior must be upwards. Therefore, the function must be of the form:

`y=(x-a)^2(x-b)^2`

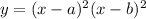
We will use a = -1 and b = 1:

`y=(x+1)^2(x-1)^2`

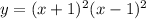
The graph is: