Question

Find the product of the complex numbers. Leave your answer in polar form

Answer 1

Given: Two complex numbers below

`\begin{gathered} z_1=2+2i \\ z_2=-3+3i \end{gathered}`

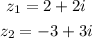
To Determine: The product of the given complex numbers

`z_1z_2=(2+2i)(-3+3i)`
`\begin{gathered} z_1z_2=2(-3+3i)+2i(-3+3i) \\ z_1z_2=-6+6i-6i+6i^2 \\ z_1z_2=-6+6i^2 \end{gathered}`

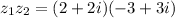
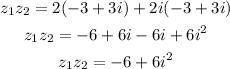
Please note that

`\begin{gathered} i=\sqrt[]{-1} \\ i^2=(\sqrt[]{-1})^2_{} \\ i^2=-1 \end{gathered}`

Therefore:

`\begin{gathered} z_1z_2=-6+6i \\ z_1z_2=-6+6(-1) \\ z_1z_2=-6-6 \\ z_1z_2=-12+0i \end{gathered}`

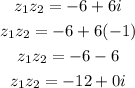
Let us convert the product to polar form

Please note that

`\begin{gathered} if,z=x+iy,the\text{ polar form is} \\ z=r(\cos \theta+i\sin \theta) \\ \text{where} \\ r=\sqrt[]{x^2+y^2} \\ \tan \theta=(y)/(x) \\ \theta=tan^(-1)((y)/(x)) \end{gathered}`

Apply the conversion into the product we got

`\begin{gathered} z_1z_2=-12+0i,x=-12,y=0 \\ r=\sqrt[]{x^2+y^2}=\sqrt[]{(-12)^2+0^2} \\ r=\sqrt[]{144+0} \\ r=\sqrt[]{144} \\ r=12 \\ \theta=\tan ^(-1)((0)/(-12)) \\ \theta=\tan ^(-1)(0) \\ \theta=\pi \end{gathered}`

Therefore:

`\begin{gathered} z_1z_2=r(\cos \theta+i\sin \theta) \\ r=12,\theta=\pi \\ z_1z_2=12(\cos \pi+i\sin \pi) \end{gathered}`

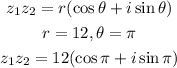
Hence, the product of the complex numbers in polar form is

12(cosπ+isinπ)