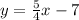Question

What equation represents a line which is parallel to the line y=5/4x - 7

Answer 1

A characteristic of parallel lines is that they have the same slope.

So for the line

`y=(5)/(4)x-7`

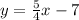
The slope is

`m=(5)/(4)`

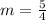
Any line parallel to this one will have the same slope:

`y=(5)/(4)x+b`

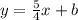
Foe example, let's say that the parallel line has to pass through the point (2,3)

Using the point slope form you can determine the equation as:

`\begin{gathered} y-y_1=m(x-x_1) \\ y-3=(5)/(4)(x-2) \\ y-3=(5)/(4)x-(5)/(2) \\ y=(5)/(4)x-(5)/(2)+3 \\ y=(5)/(4)x+(1)/(2) \end{gathered}`

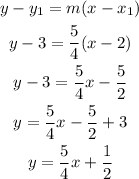
The line

`y=(5)/(4)x+(1)/(2)`

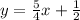
is parallel to

`y=(5)/(4)x-7`