Let h is the height of the ball after t seconds
The acceleration upward = -32 feet/sec.^2
This situation must be represented by a quadratic function
The form of the function is:
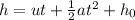
u is the initial velocity
a is the acceleration of gravity
t is the time
h0 is the initial height
From the given, the initial height is 1 foot
The acceleration of gravity is a constant value -32 ft/s^2
The initial velocity is unknown
Let us substitute the values given in the function
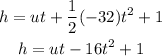
Let us arrange the terms from greatest power of t
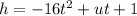
We have only 1 function in the choices similar to our function
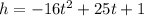
The answer is the second choice