Answer:
• Vertex: (5, –1)
,
• No symmetry
,
• Transformations: 5 units to the right, and 1 unit down.
Explanation
We are given the parent function f(x)= |x| and the transformed function:

Thus, we can get the vertex considering that a function in the form:
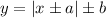
has a vertex at (+a, ±b).
Therefore, our vertex is at (5, –1). Additionally, as an absolute function has the form of a 'v', and as the vertex is at (5, –1) then it has no symmetry about the x-axis, nor y-axis, and nor about the origin, meaning it has no symmetry.
Finally, the transformation from the parent function is a shift 5 units to the right and one unit down.