The line is:
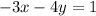
Which is equivalent to:
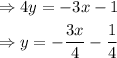
Thus, the slope of the line is equal to -3/4
a) Every line parallel to that one has the same slope, then the answer is -3/4
b) On the other hand, if m_1 and m_2 are the slopes of two perpendicular lines, then:

Therefore, since the slope of our line is equal to -3/4, the slope of any line perpendicular to that one is:
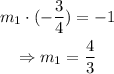
Hence, the answer is 4/3