Question

1. Use the image below to find the midpoint of segments BD and AC B 5 С D -5 4 3 2 1 1 2 3 4 5 2. Classify triangle ABC as either equilateral, right, isosceles, or none. 5 C B 2 A -3 -2 -1 2 3 4 5 6 -2

Answer 1

1. We have that B (-2,4) and D (2,1), then the midpoint has coordinates

`\begin{gathered} x=(-2+2)/(2)=0 \\ y=(4+1)/(2)=(5)/(2) \end{gathered}`

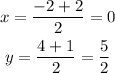
and the midpoint is (0,5/2).

On the other hand A (-4,1) and C (4,4), so the midpoint has coordinates

`\begin{gathered} x=(-4+4)/(2)=0 \\ y=(1+4)/(2)=(5)/(2) \end{gathered}`

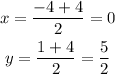
and the midpoint is (0, 5/2).

In conclusion, the midpoint of segments BD and AC is (0,5/2).

2. To classify the triangle we need to know the length of its sides

`\begin{gathered} \bar{AB}=\sqrt[]{(3-(-2))^2+\mleft(0+2\mright)^2}=\sqrt[]{25+4}=\sqrt[]{29} \\ \bar{BC}=\sqrt[]{(2-(-2))^2+(4-2)^2}=\sqrt[]{16+4}=\sqrt[]{20} \\ \bar{AC}=\sqrt[]{(3-2)^2+(4-0)^2}=\sqrt[]{1+16}=\sqrt[]{17} \end{gathered}`

Since neither of its sides has equal length, then it is not equilateral os isosceles. Besides,

`17^2+20^2\\e29^2`

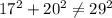
Then it is not a right triangle.

In conclusion the answer is none of the options