How many, and what type of solutions, does3x2−x−5=0 have? 2 irrational solutions 2 rational solutions 1 rational solution 2 non-real solutions

Question

asked Nov 14, 2023 184k views

1 Answer

Atif Imran · Answer 1 · 2023-11-18T02:33:38+0000

Answer:

2 irrational solutions

Explanation:

using the quadratic formula:

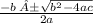
$\frac{ -b \:± \sqrt{b {}^(2) - 4ac } }{2a}$

3x²−x−5=0

where a = 3, b = -1 and c = -5, plug in those values in the quadratic formula

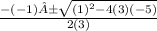
$\frac{ - ( - 1)±\sqrt{(1) {}^(2) - 4(3)( - 5) } }{2(3)}$

you get two solutions:

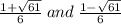
$(1 + √(61) )/(6) \: and \: (1 - √(61) )/(6)$

both can be written as:

(1± √(61) )/(6)

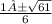
They are irrational as they cannot be written in the form p/q where p and q are whole numbers (integers)