The axis of symmetry of a parabola is a vertical line that divides the parabola into two congruent halves.
The axis of symmetry always passes through the vertex of the parabola.
The x -coordinate of the vertex is the equation of the axis of symmetry of the parabola.
A general graph of a vertical parabola is shown below:
Note there are two points x1 and x2 that have the same y-coordinate. These points are equidistant from the axis of symmetry. So, if we are given the coordinates of the points, we can find the axis of symmetry by calculating their average.
We are given the points (-2.5, 3) and (-4.5, 3).
Since they have the same y-coordinate, we calculate the average of the x-coordinates as follows:
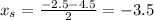
Thus, the axis of symmetry of the parabola is x = -3.5