Given:
• Starting salary of each Job = $65000
,
• Job 1 promises a $3250 raise per year
,
• Job 2 promises a 4% raise each year.
Let's complete the given tables.
The equation to represent job 1 will be a linear equation:
y = 3250t + 65000
The equation which represents job 2 will be an exponential equation:
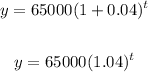
Now, to complete the tables, input the different values of t into the equation and solve for y.
• For Job 1, we have the following:
• When t = 1:
y = 3250(1) + 65000 = 68250
• When t = 5:
y = 3250(5) + 65000
y = 16250 + 65000
y = 81250
• When t = 10:
y = 3250(10) + 65000
y = 32500 + 65000
y = 97500
• When t = 15:
y = 3250(15) + 65000
y =48750 + 65000
y = 113750
• When t = 20:
y = 3250(20) + 65000
y = 65000 + 65000
y = 130000
• For Job 2, we have the folllowing:
• When t = 1:
y = 65000(1.04)¹
y = 67600
• When t = 5
y = 65000(1.04)⁵
y = 65000(1.216652902)
y = 79082
• When t = 10:
y = 65000(1.04)¹⁰
y = 65000(1.480244285)
y = 96216
• When t = 15:
y = 65000(1.04)¹⁵
y = 65000(1.800943506)
y = 117061
• When t = 20
y = 65000(1.04)²⁰
y = 65000(2.191123143)
y = 142423
Therefore, we have the complete table below: