Since triangle, ABC is an isosceles triangle because AB = BC
Then the angles of its base are equal
Since the angles of its bases are <2 and <4, then

Since <3 and <4 are vertically opposite angles
Since the vertically opposite angles are equal in measures, then
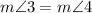
Since measure of <3 = 2x + 12, them
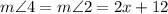
Since <1 and <2 are linear angles
Since the sum of the measures of the linear angles is 180 degrees, then

Since m<1 = 5x, then
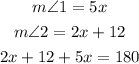
Add the like terms on the left side
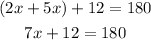
Subtract 12 from both sides
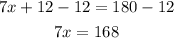
Divide both sides by 7
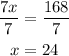
Then substitute x by 24 in the measure of <2
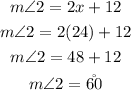
The measure of angle 2 is 60 degrees