We will assume that we want to know if the system of equations is independent or dependent:
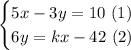
where k is a real number. We will try to find the solutions to the system, and we will try to give values to k for which the system becomes independent or dependent.
We will use substitution, we solve for the variable x on the first equation to obtain:
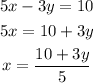
And now we replace it onto the second equation:
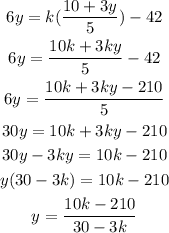
And the value of x will be:
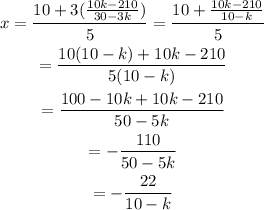
This means that a solution of the system will be:
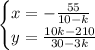
Now, for finding the values which make the system dependent. This happens when the lines have the same slope, this is, when:
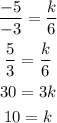
We did the division of the opposite of the coefficient of x, over the coefficient of y. This means that the system will be independent for each value of k different than 10, and will be dependent for k=10.