Question

14 Find the percent increase or decrease for each of the following values (indicate whether each is an increase or a decrease). a. 4x to x/ b. 0.25m to 0.5m 5 c. + 2p to d.y to 0.687 8 р 15 Consider the following relationships. TI. 1

Answer 1

The percentage increase or decrease is given by

`\frac{final\: \text{amount}-original\: \text{amount}}{original\: \text{amount}}*100\%`

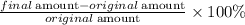
Let us find the percentage increase or decrease for the given cases.

a) 4x to x

`\begin{gathered} (x-4x)/(4x)*100\% \\ (-3x)/(4x)*100\% \\ -0.75*100\% \\ -75\% \end{gathered}`

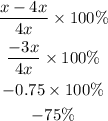
Therefore, it is a percentage decrease (-75%) since it is negative.

b) 0.25m to 0.5m

`\begin{gathered} (0.5m-0.25m)/(0.25m)*100\% \\ (0.25m)/(0.25m)*100\% \\ 1*100\% \\ 100\% \end{gathered}`

Therefore, it is a percentage increase (100%) since it is positive.

c) 1/2p to 5/8p

`\begin{gathered} ((5)/(8)p-(1)/(2)p)/((1)/(2)p)*100\% \\ ((1)/(8)p)/((1)/(2)p)*100\% \\ (1)/(8)*(2)/(1)*100\% \\ (2)/(8)*100\% \\ (1)/(4)*100\% \\ 25\% \end{gathered}`

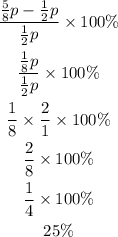
Therefore, it is a percentage increase (25%) since it is positive

d) y to 0.68y

`\begin{gathered} (0.68y-y)/(0.68y)*100\% \\ (-0.32y)/(0.68y)*100\% \\ -0.47*100\% \\ -47\% \end{gathered}`

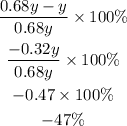
Therefore, it is a percentage decrease (-47%) since it is negative.