The equation
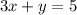
has two variables: x and y.
And since we have only one equation, the variables have infinite possible values, which are related to that equation.
Another way of seeing that is by calling x the independent variable, and then y will be the dependent variable (its value depends on the value of x).
So, we can isolate y on the left side of the equation, to obtain:
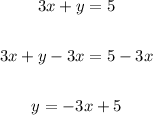
Now, we see that the above equation represents a line (an infinite set of points), that has a slope -3 and a y-intercept 5.
Therefore, all the points on that line are solutions to the given equation.
If we graph that set of solutions on a xy-plane, we obtain the line below: