Question

Please help me help help me please help help me out

Answer 1

`f^(-1)(x)=(x-4)^3+1`

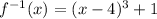
1) We can find the inverse function, by following some steps. So let's start with swapping the variables this way:

`\begin{gathered} f(x)=\sqrt[3]{x-1}+4 \\ y=\sqrt[3]{x-1}+4 \end{gathered}`

2) Now let's isolate that x variable getting rid of that cubic root:

`\begin{gathered} x=\sqrt[3]{y-1}+4 \\ x-4=\sqrt[3]{y-1} \\ (x-4)^3=(\sqrt[3]{y-1})^3 \\ (x-4)^3=y-1 \\ y=(x-4)^3+1 \end{gathered}`

Note that when we isolate the y on the left we had to adjust the sign dividing it by -1, to get y, not -y.