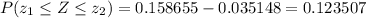Since this is a normal distribution, the area between the z-scores z₁ = 1 and z₂ = 1.81 is just the probability that the random variable Z is between z₁ and z₂:
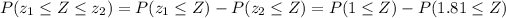
Using the values reported on tables for the standardized normal distribution, we know that:
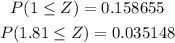
Now, using these results: