Question

Given the following expressions, you will identify the followingslope, y- intercept , x intercept, domain range , and is the function increasing or decreasing

Answer 1

Given the following function:

`\text{ 3x - 2y = 16}`

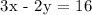
A.) SLOPE

Let's first transform the given equation into the standard slope-intercept form: y = mx + b

Because the m in the equation represents the value of the slope.

We get,

`\begin{gathered} \text{ 3x - 2y = 16} \\ \text{ (3x - 2y = 16)( -}\frac{\text{ 1}}{\text{ 2}}) \\ \text{ -}(3)/(2)x\text{ + y = -}(16)/(2) \\ \text{ -}(3)/(2)x\text{ + y = -}8 \\ \text{ y = }(3)/(2)x\text{ - 8} \end{gathered}`

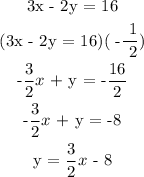
The slope-intercept form of 3x - 2y = 16 is y = (3/2)x - 8. Where m = 3/2.

Therefore, the slope of the function is 3/2.

B.) Y - INTERCEPT

In the standard slope-intercept form : y = mx + b, b represents the y - intercept.

Therefore, in the converted form of the function y = (3/2)x - 8. b is equals to -8.

The y-intercept is 0, -8.

C.) X - INTERCEPT

The x - intercept is the point at y = 0.

We get,

`\text{ 3x - 2y = 16}`
`\text{ 3x - 2(0) = 16}`
`\text{ 3x = 16}`
`\text{ }\frac{\text{3x}}{3}\text{ = }\frac{\text{16}}{3}`
`\text{ x = }\frac{\text{ 16}}{\text{ 3}}`

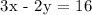
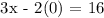
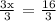
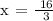
Therefore, the x - intercept is 16/3, 0

D.) DOMAIN RANGE

The function has no undefined points nor domain constraints. Therefore, the domain is

[tex]-\infty\: We usually encounter undefined points when a given value of x will make the denominator equal to zero (0).

Example: 2/(3 - x) at x = 3 is undefined.

E.) INCREASING OR DECREASING

The easiest way to determine if the function is decreasing or increasing is by looking at the slope (m). If the slope is greater than 0 (m > 0) or a positive, the function is increasing. If the slope is less than 0 (m < 0) or a negative, the function is decreasing.

Here, the slope is 3/2 which we first solved. Since the slope is greater than zero or a positive, the function is, therefore, increasing.

The answer is increasing.