Answer:
y = 0.5x + 5
Step-by-step explanation:
The equation of a line can be calculated as:

Where m is the slope and (x1, y1) is a point in the line.
To find the slope of our line, we need to identify the slope of the given line.
Since the equation of the given line is y = -2x + 1, the slope of this line is -2, because it is the number beside the x.
Then, two lines are perpendicular if the product of their slopes is equal to -1. So, we can write the following equation:
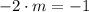
Therefore, the slope m of our line will be:
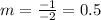
Now, we can replace the value f m by 0.5 and the point (x1, y1) by (0, 5) and we get that the equation of the line is:
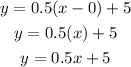
Therefore, the answer is y = 0.5x + 5