Given:

Required:
We need tofnind the vertical asymptote(s) and hole (s) for the graph of the given function.
Step-by-step explanation:
Vertical asymptotes can be found when the numerator of the function is equal to zero.
The numerator of the given function is (x+4)(x+1)
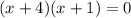

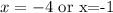
The asymptote of the given function is either x =-4 or x =-1.
Recall that a hole exists on the graph of a rational function when both the numerator and denominator of the function are equal to zero.
The common factor of the given rational function