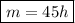Question

2.) The information in the table below shows the

distance a car traveled during a number of hours.
Hours (h)
Miles (m)
1
45
2
90
3
135
4
180
Write an equation using the variables h and m that
represents the information in the table

Answer 1

m = 45h

Explanation:

Calculate the difference in y-values (miles):

`45 \underset{+45}{\longrightarrow} 90\underset{+45}{\longrightarrow} 135\underset{+45}{\longrightarrow} 180`

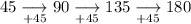
As the number of miles increases by the same amount for every increase of an hour, the equation is linear.

`\boxed{\begin{minipage}{6.3 cm}\underline{Slope-intercept form of a linear equation}\\\\$y=mx+b$\\\\where:\\ \phantom{ww}$\bullet$ $m$ is the slope. \\ \phantom{ww}$\bullet$ $b$ is the $y$-intercept.\\\end{minipage}}`

Given variables:

• x = Hours (h)
• y = Miles (m)

As the number of miles increases by 45 miles for each increase of an hour, the slope of the linear equation is 45:

`\implies m=45h+b`

To find b, substitute one of the ordered pairs into the equation and solve for b:

`\implies 45=45(1)+b`

`\implies 45=45+b`

`\implies b=45-45`

`\implies b=0`

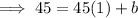
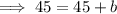
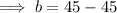
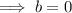
Therefore, the equation using the variables h and m that represents the information in the given table is:

`\boxed{m=45h}`