Thomas is buying football jerseys for his high school football team.
The cost of each jersey is $80.
The company also charges a processing fee of $100.
We could write an equation that models Thomas's total cost for purchasing x
number of jerseys.
Since for every x jerseys Thomas buys, he pays

But he also has to pay the company's processing fee, this is independent of the quantity bought.
So, the total cost for buying x number of jerseys is;
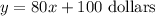
ii. What is Thomas's total cost, if he buys 55 jerseys?
We can use our formula,
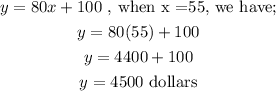
Therefore, Thomas's total cost for 55 jerseys is $4500