Question

What is the value of x in the triangle?a right triangle with a short leg of length x and hypotenuse of length 3 times the square root of 2A. B. C. D. E.

Answer 1

Given the right triangle below:

To solve for x, we use the trigonometric ratio.

In the above triangle, the angles at A and B are equal.

Thus, we have

`\begin{gathered} \angle A+\angle B+\angle C=180(su\text{m of angles in a triangle\rparen} \\ \angle A=\angle B \\ thus, \\ 2\angle\text{B+90=180} \\ \Rightarrow2\angle\text{B=180-90} \\ 2\angle\text{B=90} \\ \Rightarrow\angle\text{B=45} \end{gathered}`

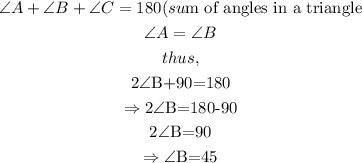
From trigonometric ratio,

`\sin\theta\text{=}(opposite)/(hypotenuse)`

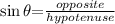
In this case, θ is the angle at B, which is 45; opposite is AC, and hypotenuse is AB.

Thus,

`\begin{gathered} \sin45=(x)/(3√(2)) \\ \Rightarrow x=3√(2)*\sin45 \\ =3√(2)*(1)/(√(2)) \\ =3 \end{gathered}`

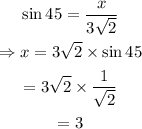
Hence, the value of x is

`3`

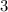
The correct option is B