Question

At a carnival, there is a game where you can draw one of 10 balls from a bucket if you pa $16. The balls are numbered from 1 to 10. If the number on the ball is even, you win $22 If the number on the ball is odd, you win nothing. If you play the game, what is the expected profit?

Answer 1

`\text{\$-5}`

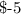
Step-by-step explanation

To find the expected profit, we have to first find the expected payout.

There is a possibility of drawing up to 10 balls, numbered 1 to 10.

There are 5 even balls and 5 odd balls.

We have to find the probabilty of drawing even or odd balls:

=> The probability of drawing an even ball is:

`P(\text{even)}=(5)/(10)=(1)/(2)`

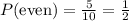
=> The probability of drawing an odd ball is:

`P(\text{odd)}=(5)/(10)=(1)/(2)`

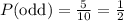
The expected payout is the sum of the product of the probability of drawing each ball and the prize of each ball.

That is:

`\begin{gathered} E(X)=\Sigma\mleft\lbrace X\cdot P(X)\mright\rbrace \\ E(X)=(22\cdot(1)/(2))+(0\cdot(1)/(2)) \\ E(X)=11+0 \\ E(X)=\text{ \$11} \end{gathered}`

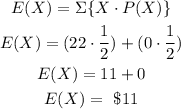
The expected profit can be found by subtracting the cost of playing the game from the expected payout:

`\begin{gathered} Exp.Profit=11-16 \\ Exp.Profit=\text{ \$-5} \end{gathered}`

That is the answer.