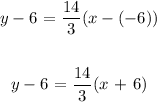Question

what's the equation of the line that passes through the points (-9,-8) and (-6,6) in point slope form

Answer 1

The equation of the line passing through the given points in the point slope form is;

`y-6\text{ = }(14)/(3)(x\text{ + 6)}`

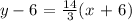
Here, we want to find the equation of the line that passes through the given points

Mathematically, we can write the equation of a line as follows in point slope form;

`y-y_1=m(x-x_1)`

m here represents the slope of the line

To calculate m which is the slope, we use the slope equation as follows;

`\begin{gathered} m\text{ = }(y_2-y_1)/(x_2-x_1) \\ \\ m\text{ = }(6-(-8))/(-6-(-9))\text{ = }\frac{6\text{ + 8}}{-6\text{ + 9}}\text{ = } \\ =\text{ }(14)/(3) \end{gathered}`

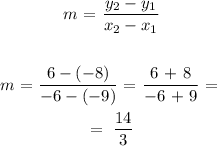
To write the equation, we use any of the two given points.

Thus, we have;

`\begin{gathered} y-6\text{ = }(14)/(3)(x-(-6)) \\ \\ y-6\text{ = }(14)/(3)(x\text{ + 6)} \end{gathered}`