Question

I just need part c please The first one I know it’s 32

Answer 1

We are given that in a falling object the distance "d" is directly proportional to the square of the time and the proportionality constant is 16. This means that the function of distance is given by:

`d(t)=16t^2`

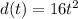
The average rate of change is given by the following formula:

`r=(d(t_f)-d(t_0))/(t_f-t_0)`

Where:

`t_f,t_0=\text{ final and initial time}`

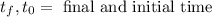
Now, we substitute the values of "d(t)":

`r=(16t_f^2-16t_0^2)/(t_f-t_0)`

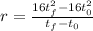
We can factor the numerator and we get:

`r=16((t_f-t_0)(t_f+t_0))/(t_f-t_0)`

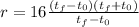
Simplifying we get:

`r=16(t_f+t_0)`

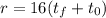
For the first 2 seconds we have:

`\begin{gathered} t_0=0 \\ t_f=2s \end{gathered}`

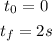
Substituting the values we get:

`\begin{gathered} r=16(2s+0s) \\ r=32 \end{gathered}`

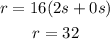
Therefore, the average rate of change is 32

For the next 2 seconds we have:

`\begin{gathered} t_0=2s \\ t_f=4s \end{gathered}`

Now, we substitute the values:

`\begin{gathered} r=16(4s+2s) \\ r=96 \end{gathered}`

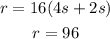
Therefore, the rate of change in the next two seconds is 96.

For the next 2 seconds we have:

`\begin{gathered} t_0=4s \\ t_f=6s \end{gathered}`

Substituting the values we get:

`\begin{gathered} r=16(6s+4s) \\ r=160 \end{gathered}`

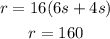
Therefore, the rate of change is 160