Given that 'M' varies directly with the square of 'd',
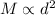
Given that 'M' varies inversely with the square root of 'x',
![M\propto\frac{1}{\sqrt[]{x}}](https://img.qammunity.org/2023/formulas/mathematics/college/w3np04aeqhdni9m69ahb34s0naqo49hc0m.png)
Combining the relationships,
![M\propto\frac{d^2}{\sqrt[]{x}}](https://img.qammunity.org/2023/formulas/mathematics/college/olh95c0lb145fafzxdqwgh5frmcjbs0fbz.png)
Let 'k' be the constant of proportionality. Then,
![M=k\cdot\frac{d^2}{\sqrt[]{x}}](https://img.qammunity.org/2023/formulas/mathematics/college/d69meavowmhsmsxe8dj4xr3i3o6rbc9daz.png)
Given that M=12 when d=3 and x=4,
![\begin{gathered} 12=k\cdot\frac{(3)^2}{\sqrt[]{4}} \\ 12=k\cdot(9)/(2) \\ k=(12\cdot2)/(9) \\ k=(8)/(3) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/kp4awxcvuo9lfqt33zsreabxudau2j15qc.png)
Substitute the value of this constant in the general expression,
![M=(8)/(3)\cdot\frac{d^2}{\sqrt[]{x}}](https://img.qammunity.org/2023/formulas/mathematics/college/cbnvmsnm9x997sn9hz1vxedfnx0vievf7a.png)
Thus, the required general formula to describe the relation is obtained as,
![M=(8)/(3)\cdot\frac{d^2}{\sqrt[]{x}}](https://img.qammunity.org/2023/formulas/mathematics/college/cbnvmsnm9x997sn9hz1vxedfnx0vievf7a.png)