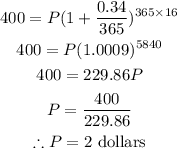Question

Paisley is going to invest in an account paying an interestrate of 34% compounded daily. How much would Paisleyneed to invest, to the nearest dollar, for the value of theaccount to reach $400 in 16 years?

Answer 1

$2

Step-by-step explanation:

To solve the given problem, we'll use the below compound interest formula;

`A=P(1+(r)/(n))^(nt)`

where A = future amount = $400

P = the initial amount( principal)

r = annual interest rate in decimal form = 34/100 = 0.34

n = number of compounding periods in a year = 365

t = time in years = 16

Let's go ahead and substitute the above values into our formula and solve for P;

`\begin{gathered} 400=P(1+(0.34)/(365))^(365*16) \\ 400=P(1.0009)^(5840) \\ 400=229.86P \\ P=(400)/(229.86) \\ \therefore P=2\text{ dollars} \end{gathered}`