Question

Simplify. In the form of a paragraph, explain in complete sentences the steps necessary to simplify the expression andinclude the final answer in your explanation. Complete your work in the space provided or upload a file that can displaymath symbols if your work requires it.

Answer 1

`((x^3y)/(xy^2))^(-2)`

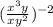
1. When dividing with exponents, the exponent of a variable in the denominator is subtracted from the exponent in the numerator for the same variable. Then, first step to simplify is subtract the exponents of x and y in the fraction in parentheses:

`\begin{gathered} =(x^(3-1)y^(1-2))^(-2) \\ =(x^2y^(-1))^(-2) \end{gathered}`

2. To remove the parentheses you multiply each exponent in the parentheses by the exponent out of the parentheses:

`\begin{gathered} =x^(2\cdot(-2))y^((-1)\cdot(-2)) \\ \\ =x^(-4)y^2 \end{gathered}`

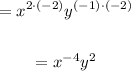
3. When you have a negative exponent (as the x powered to -4) you divide 1 in to the term with negative exponent (after you divide the exponent turns into a positive exponent):

`=(1)/(x^4)\cdot y^2`

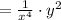
4. Then, the given expression simplified is:

`((x^3y)/(xy^2))^(-2)=(y^2)/(x^4)`