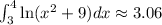The Trapezoidal rule formula is given to be:
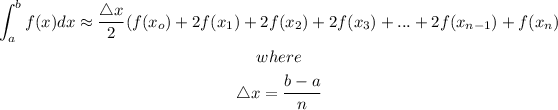
The question gives:
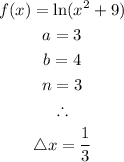
Therefore, divide the interval into n = 3 subintervals of length 1/3 with the following endpoints:
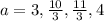
Evaluate the function at the endpoints:
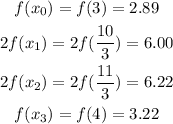
Sum up the calculated values and multiply by Δx/2:
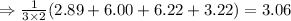
Therefore, the answer will be: