Answer:
The standard deviation of the population = 6.08
Explanations:
The given ages of the employers are:
31, 41, 35, 22, 38, 31
Find the mean of the dataset:
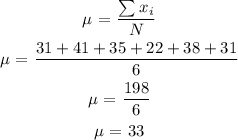
Find the summation of the square of each deviation from the mean
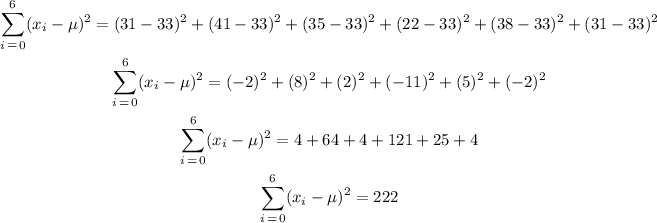
The standard deviation is given by the formula:
![\begin{gathered} \sigma\text{ = }\sqrt[]{\frac{\sum ^{}_{}(x_i-\mu)^2}{N}} \\ \sigma\text{ = }\sqrt[]{(222)/(6)} \\ \sigma\text{ = }\sqrt[]{37} \\ \sigma\text{ = }6.08 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ix0xs5alv8vyvud81aghm2oejskt2cbfcr.png)
The standard deviation of the population = 6.08 (rounded to 2 decimal places)