Answer:
0.8486
Step-by-step explanation:
To find the probability that a score will be between 70 and 93, we first need to standardize these values, so we will use the following

Therefore, for 70 and 93, we get
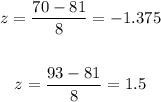
Then, we need to find the following probability
P(-1.375 < z < 1.5)
This probability can be calculate using a standard normal table, so
P(-1.375 < z < 1.5) = P(z < 1.5) - P(z < -1.375)
P(-1.375 < z < 1.5) = 0.9332 - 0.0846
P(-1.375 < z < 1.5) = 0.8486
Therefore, the probability is 0.8486