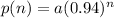Question

Enter an equation for the function. Give your answer in the form a(6"). In theevent that a = 1, give your answer in the form b".A laser beam with an output of 4 milliwatts is directed into a series of mirrorsThe laser beam loses 6% of its power every time it reflects off of a mirror. Thepower p(n) is a function of the number n of reflections.The equation is p(n) = 0

Answer 1

From the data provided, we have the following;

Initial power output = 4 milliwatts

Power lost per reflection = 6% (OR 0.06)

We need to find a function that shows the power each time the laser beam is reflected off a mirror.

Note that the general equation for an exponential decay/loss is given as;

`\begin{gathered} y=a(1-r)^x \\ OR \\ f(x)=a(1-r)^x \end{gathered}`

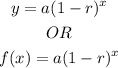
Note also that (1 - r) is often replaced by b. Therefore, the equation can be written as;

`\begin{gathered} f(x)=a(1-r)^x^{} \\ f(x)=ab^x \end{gathered}`

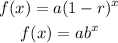
Where the number of reflections is given by n and p(n) is a function of the number of reflections, we now have;

`p(n)=ab^n`

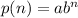
Where the variables are;

`\begin{gathered} a=4\text{ milliwatts (initial value)} \\ r=0.06 \end{gathered}`

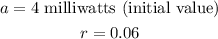
We now have the function as;

`\begin{gathered} p(n)=a(1-0.06)^n \\ p(n)=a(0.94)^n \end{gathered}`

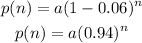
ANSWER:

`p(n)=a(0.94)^n`