Question

The senior classes at High School A and High School B planned separate trips to New York City.The senior class at High School A rented and filled 2 vans and 6 buses with 366 students. HighSchool B rented and filled 6 vans and 3 buses with 213 students. Each van and each bus carriedthe same number of students. Find the number of students in each van and in each bus.Answer: A van hasstudents and bus has students

Answer 1

Let V be the number of students that fit inside a van and B the number of students that fit inside a bus. Since 366 students fit in 2 vans and 6 buses, then:

`2V+6B=366`

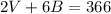
Since 213 students fit in 6 vans and 3 buses, then:

`6V+3B=213`

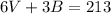
Multiply the second equation by 2:

`\begin{gathered} 2(6V+3B)=2(213) \\ \Rightarrow12V+6B=426 \end{gathered}`

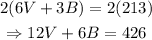
Then, we have the system:

`\begin{gathered} 2V+6B=366 \\ 12V+6B=426 \end{gathered}`

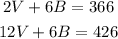
Substract the first equation from the second one and solve for V:

`\begin{gathered} (12V+6B)-(2V+6B)=426-366 \\ \Rightarrow12V-2V+6B-6B=60 \\ \Rightarrow10V=60 \\ \Rightarrow V=(60)/(10) \\ \therefore V=6 \end{gathered}`

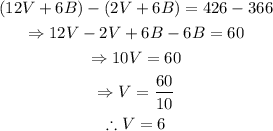
Substitute V=6 into the first equation and solve for B:

`\begin{gathered} 2V+6B=366 \\ \Rightarrow2(6)+6B=366 \\ \Rightarrow12+6B=366 \\ \Rightarrow6B=366-12 \\ \Rightarrow6B=354 \\ \Rightarrow B=(354)/(6) \\ \therefore B=59 \end{gathered}`

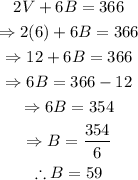
Therefore, a van has 6 students and a bus has 59 students.