Question

Find the distance between the points. Round to the nearest tenth if necessary. (3, 7), (-5, -7) Distance?

Answer 1

To find the distance between both points you have to apply pythagoras theorem.

First draw both points and form a rigth triangle with the distance between them as the hypothenuse:

The length of the base of the triangle "a" is determined by the difference between the x-coordinates of both points:

`a=x_2-x_1=3-(-5)=3+5=8`

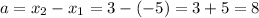
The heigth of the triangle "b" is determined by the difference between the y-coordinates of both points:

`b=y_2-y_1=7-(-7)=7+7=14`

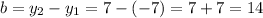
Now using phytagoras theorem you can calculate the length of the hypotenuse as:

`\begin{gathered} a^2+b^2=c^2 \\ (8)^2+(14)^2=c^2 \\ c^2=260 \\ c=\sqrt[]{260} \\ c=2\sqrt[]{65}=16.12 \end{gathered}`

The distance between points (3,7) and (-5,-7) is 2√65